Thales von Milet

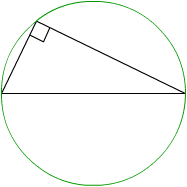
Thales ist der erste heute noch bekannte griechische Mathematiker. Mindestens fünf geometrische Grundregeln sollen von ihm entdeckt und angewandt worden sein. Am bekanntesten ist Thales für einen speziellen Kreis, der nach ihm Thaleskreis genannt wird. Thales hat nämlich herausgefunden, dass die Hypotenuse jedes rechtwinkligen Dreiecks mit dem Durchmesser eines Kreises zusammenfällt, auf dem auch die Ecke mit dem rechten Winkel zu liegen kommt.

Thales arbeitete als Ingenieur und benützte die Geometrie vor allem um sie anzuwenden. Den Thaleskreis zum Beispiel probierte er mit vielen rechtwinkligen Dreiecken aus. Als er dann sah, dass er bei all seinen Experimenten funktionierte, benutzte er ihn für seine Berechnungen. Für ihn stellte sich noch nicht die Frage nach einem mathematisch korrekten Beweis. Ich will dir nun auf eine Art, wie es auch Thales gemacht haben könnte, zeigen, dass die Idee des Thaleskreis korrekt ist.

Als erstes brauchst du ein rechtwinkliges Blatt Papier. Eine Seite aus dem IKEA Katalog geht bestens - mach einfach sicher, dass das Papier rechtwinklig ist.

 

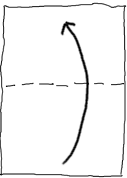
Falte das Blatt nun an einer der Diagonalen. Öffne es wieder und falte die Seite an der zweiten Diagonalen. Wenn du jetzt die zwei Diagonalen nicht gut siehst, kannst du sie mit einem Lineal und Bleistift nachzeichnen.

Als nächstes braucht es einen Falt in der Mitte,
so dass du ein kleineres Rechteck bekommst.

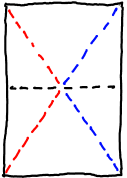
Zusammengefalten liegen die Diagonalen jetzt aufeinander. Im Bild links kommen die zwei roten Teilstücke aufeinander zu liegen. Das gleiche ist mit den blauen der Fall. Sie decken sich, das heisst, sie haben die gleiche Länge.

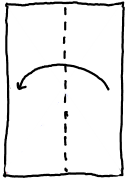
Öffne das Papier und halbiere es in die andere Richtung ...

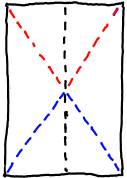
und ja - die Diagonalen liegen wieder aufeinander.
 

Dieses kleine Experiment zeigt, dass die Teilstücke der Diagonalen in einem Rechteck alle gleich lang sind: Wenn das Papier zusammengefaltet ist, liegen sie aufeinander. Wenn du mir noch nicht glaubst kannst du es ja, wie Thales es gemacht hätte, an ein paar weiteren Rechtecken ausprobieren. Oder wenn es dir lieber ist, so versuche einen mathematischen Beweis zu finden, zum Beispiel mit Hilfe von ähnlichen Dreiecken.

Du wunderst dich nun vielleicht, was Rechtecke mit dem Thaleskreis zu tun haben. Naja - wenn du ein rechtwinkliges Dreieck nimmst, es verdoppelst, das zweite um 180° drehst und schliesslich die beiden Dreiecke an der Hypotenuse zusammenfügst, so hast du ein Rechteck.

Links siehst du ein Bild eines solchen Rechtecks. (Wenn du mit der Maus darüber fährst, kannst du die Proportionen ändern.) Im Bild sind auch noch die Geraden von den rechen Winkeln zur Mitte der Hypotenusen eingezeichnet. Diese bilden zusammen die eine Diagonale des Rechtecks - die Hypotenusen die andere.

Wir haben oben herausgefunden, dass die Teilstücke der Diagonalen alle die gleiche Länge haben. Der Schnittpunkt der beiden Diagonalen ist also von allen Ecken gleich weit entfernt. Die Menge aller Punkte, die von einem gegebenen Punkt eine gegebene Distanz entfernt sind, liegen auf einem Kreis. Die Ecken des Rechtecks liegen also auf einem Kreis, dessen Zentrum der Schnittpunkt der Diagonalen ist. Wenn du nun eines der beiden rechtwinkligen Dreiecke anschaust, siehst du, dass alle Ecken auf einem Kreis liegen und dass der Kreismittelpunkt mit dem Mittelpunkt der Hypotenuse zusammenfällt. Dies entspricht der Aussage des Thales-Satzes.

Die Animation zeigt dir noch einmal, dass das Dreieck rechtwinklig bleibt, wenn die dritte Ecke auf dem Thaleskreis liegt. Probiere es aus indem du mit der Maus das Dreieck veränderst.

Zurück Weiter