
| |
Thales of Milet
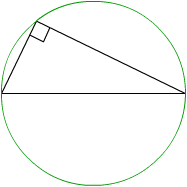
Thales is the first Greek mathematician we know about. Five Euclidean theorems which we still learn today were discovered and applied by Thales. Probably the most famous of these theorems is that a triangle inscribed in a semicircle is a right triangle.
Thales did not prove things the way we do today - he looked at the problem - tried it out with a lot of different sizes and angles - and when he was convinced that his calculations hold he used them in his daily work as an engineer. I'm going to show you a proof in the style of Thales. Afterwards you will know for sure that a triangle inscribed into a semicircle will always be a right triangle.

To start off try to get your hands on a rectangular piece of paper. Anything will do - for example - a page from a Sears catalogue will do just fine. Just don't forget to send your thanks to Sears once you are done with it :-)
Now fold the page along the two diagonals as you can see in the picture to the right. Open it up again after each fold - the fold is just so that you can see the diagonal lines of the page. If you want to you can additionally trace the diagonals using a pencil and a ruler.
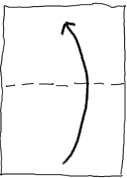
Now fold it in half so that the fold divides the page into two rectangular parts.
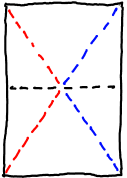
| Now if you have it folded together the half of the diagonals are on top of each other. They fit exactly onto each other and have the same length. (in the picture the red and the green half diagonals go onto each other to show that they have the same length.) |
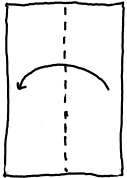
Now fold it the other way...
And yes!!! the half diagonals fit onto each other again.
| |
So this shows that the halves of the diagonals in a rectangle all have the same length. If you don't believe me go with the spirit of Thales and try out some more rectangles. Just make sure they are rectangles. Or of course - you always could bother with a formal proof - but you're on your own with that. (Tip: you may want to use similar triangles.)
|
You may wonder what a rectangle has to do with a triangle in a circle: If you take a right triangle and turn it half a rotation and then glue the two hypotenuse together you get a rectangle.
Now the center of the hypotenuse is the place where the two diagonals intersect. We know that all the pieces of the diagonals are of equal length. So as long as the hypotenuse of the right triangle stays the same, the distance from the center of the hypotenuse to the right triangle will not change either - no matter how the angles in the two smaller angles in the right triangle change. So the right angle is always a given distance form the center of the hypotenuse away. A circle is the set of all points that are at a given distance from a fixed point. So we know that all possible right angles are on a circle. (Move your mouse over the image to change the shape of the rectangle.)
Move your mouse over the above image to move the right angle along the circle. As long as the angle is on the circle it will always stay a right angle.
