| |
Benoit B. Mandelbrot
und
Waclaw Sierpinski
Mandelbrot und Sierpinski sind beide Mathematiker, die auf dem Gebiet der fraktalen
Geometrie wichtige Beiträge leisteten.
Waclaw Sierpinski lebte von 1882 bis 1969. Er war einer der berühmtesten polnischen Mathematiker. Schauen wir uns eine seiner Entdeckungen an, die nach ihm Sierpinski Dreieck genannt wird.
Das Sierpinski Dreieck hat die Eigenschaften der Fraktale:
Ein Fraktal ist eine geometrische Figur, die selbstähnlich ist und fraktale Dimensionen aufweist.
Ein Fraktal wird selbstähnlich genannt, weil seine Teile dem Ganzen ähnlich sind; schaust du dir einen Teil eines Fraktals an, so sieht er ungefähr gleich aus wie der ganze Fraktal. Das Sierpinsi Dreieck zum Beispiel kannst du vergrössern so viel du willst, es sieht immer ähnlich aus.
Von einer fraktalen Dimension sprechen wir, wenn etwas nicht ein-, zwei- oder mehrdimensional ist, sondern etwas dazwischen. Ein sehr schönes Beispiel dafür ist der Rand des Sierpinski Dreiecks. Das magische Bild zeigt dir, wie ein Sierpinski Dreieck entsteht: Wir beginnen mit einem gleichseitigen Dreieck. Dann schneiden wir ein Dreieck aus, dessen Ecken mit den Mittelpunkten der Seiten des Anfangsdreiecks zusammenfallen. Übrig bleiben drei kleinere Dreiecke. Den Ausschneideprozess nennen wir Iteration. Die Iteration ist ein Arbeitsschritt, der immer wieder ausgeführt wird. Das Gebilde, das dabei entsteht, das Sierpinski Dreieck, hat einen unendlich langen Rand: Bei jeder Iteration vergrössert sich die Länge des Randes um die Hälfte der vorherigen Iteration. Probier es auf Papier aus!
Beim üblichen Dreieck ist der Rand eindimensional. Jeder Punkt kann durch eine Zahl ausgedrückt werden, zum Beispiel als Distanz, die von einer Ecke aus der Grenze entlang im Uhrzeigersinn zurückgelegt werden muss. Wie können wir das nun beim Sierpinski Dreieck machen? Auch hier gibt es eine Möglichkeit in einem Zug der Grenze nachzugehen. Schau dir den Weg an, den wir bei einem Sierpinski Dreieck machen, nachdem es 5 Iterationen hinter sich hat.
Dieses Sierepinski Dreieck ist aber nur ein "Vorfraktal", da es nicht wirklich selbstähnlich ist;
wenn du es auch nur etwa fünfmal vergrösserst, siehst du keine
Selbstähnlichkeit mehr, sondern nur noch grosse Flächen.
Um aus diesem "Vorfraktal" ein echtes Fraktal zu erhalten, müsste es noch
durch unendlich viele Iterationen gehen.
Wie können wir nun einen Punkt beschreiben, der irgendwo auf dem Rand des Sierpinski Dreiecks liegt? Wir könnten es auf die gleiche Art versuchen wie bei einem normalen Dreieck. In einem normalen Dreieck kann man mit einer Zahl die Distanz angeben, welche man zurücklegen muss, um von einem Eckpunkt zu einem bestimmten Punkt zu gelangen, wenn man zum Beispiel im Uhrzeigersinn rum geht. Beim Sierpinskidreieck kann man auch dem Rand nachgehen; die obige Animation zeigt einen möglichen Weg. Diese Distanz ist aber abhängig von der Menge der Iterationen, die schon gezeichnet sind. Der obere Eckpunkt zum Beispiel ist nach zwei Iterationen schon mehr als doppelt so weit vom unteren Eckpunkt entfernt. Diese Distanz ist also nicht fest und hilft uns nicht weiter.
Wir könnten den Punkt auch mit zwei Zahlen festlegen, indem wir ein Koordinatensystem wählen. Ist die Grenze des Siepinski Dreiecks nun zwei- oder eindimensional? Um einen Punkt festzulegen braucht es zwei Zahlen, es ist also auf eine Art zweidimensional, andererseits gehen wir nicht von einer Dicke der Linie aus, und Linien selber sind eindimensional. Die Grenze des Sierpinski Dreiecks liegt also irgendwo dazwischen und kann nicht mit einer ganzen Zahl dargestellt werden.
In der Natur findet man viele Beispiele für fraktale Strukturen. Ein schönes Beispiel
ist der Blumenkohl. Schau dir ein kleines Blumenkohlröslein an und du wirst sehen, dass es die
gleiche Form wie der ganze Kopf hat. Das gleiche Prinzip, dass die Form eines Teiles dem ganzen
ähnlich ist, findet man auch wie schon oben erwähnt bei Küstenlinien, aber auch bei Bergen, Wolken,
Bäumen oder Farnen. Schau dir mal einen Wachholderbaum bis zum kleinsten sichtbaren Teil seiner Nadeln
an!
Es war Benoit B. Mandelbrot, der die Eigenschaften von Fraktalen definierte. Er kam 1924 in Polen
zur Welt und zog mit etwa 12 Jahren nach Frankreich.
Er führte auch die Mandelbrot Menge ein,
die einer der berühmtesten Fraktale ist.
Wir können aus jeder Grundform ein Fraktal machen, indem wir sie immer wieder reproduzieren. Überlegen wir uns einmal, wie aus einem Pythagoräischen Dreieck ein Pythagorasbaum entstehen kann. Als Anfangsbild nehmen wir ein Quadrat, dem wir ein rechtwinkliges Dreieck so anfügen, dass seine Hypotenuse einer Quadratseite entspricht. Dann bilden wir auch über den anderen Dreieckseiten Quadrate. Dies ist nun unser Ausgangsbild. Nun wiederholen wir den ganzen Prozess noch einmal, indem wir an alle Quadrate erneut Dreiecke und deren Seitenquadrate anhängen. Das können wir unendlich oft wiederholen. Was daraus entsteht, sieht aus wie ein "Pythagoräischer Blätterbaum".
Probieren wir nun noch eine kleine Variation dazu aus: Wenn wir die beiden Katheten bei jeder Runde von neuem vertauschen, so entsteht ein "Pythagoräischer Nadelbaum".
Übrigens ist bei jeder Iteration die Summe der Flächen
der neuangefügten Quadrate wieder gleich gross wie die Fläche des ursprünglichen Quadrates.
Mit dem Satz des Pythagoras können wir dies leicht beweisen.
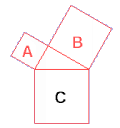
Für das Bild links gilt, dass die Quadrate A und B zusammen so gross sind wie Quadrat C.
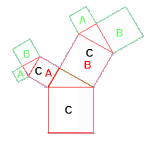
Da a²+b²=c², wissen wir, dass alle grünen Quadrate A und B
im Bild rechts zusammen die Fläche ihres Quadrat C haben.
Und da die roten Quadrate A und B
die gleiche Fläche haben wie das grosse Quadrat C, so können wir daraus schliessen, dass alle grünen
Quadrate zusammen die Fläche des grossen Quadrat C haben.
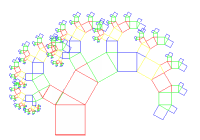
Für jede weitere Runde (Iteration) gilt natürlich wieder, dass alle neu hinzugefügten Quadrate zusammen
die Fläche des ursprünglichen Quadrates haben.
Falls du dir die beiden Pythagorasbäume noch nicht angeschaut hast, hier noch einmal die Links:
"Pythagoräischer Nadelbaum"
"Pythagoräischer Blätterbaum"
