| |
Benoit B. Mandelbrot
and
Waclaw Sierpinski
Mandelbrot and Sierpinski are two mathematicians who made important contributions in the
field of fractals.
Waclaw Sierpinski lived from 1882 to 1969. He was one of the most famous Polish mathematicians. Let's look at a discovery which was named after him the Sierpinski Triangle. He found it while reasearching on topology.
The Sierpinski Triangle has all the properties of a fractal:
A fractal is a geometric shape which is selfsimilar and which has a fractal dimension.
Selfsimilar means that when you look at a smaller part of the fractal, it still looks about the same. For example, you can magnify the Sierpinski Triangle as much as you like and it will still look about the same.
A fractal dimension means that it is not just one, two, or more dimensional, but something in between. A perfect example of this is the border of the Sierpinski triangle. Take a look at the animation which shows how it is created. To draw a Sierpinski triangle, start out with an equilateral triangle. Then, a triangle is cut out which has it's corners at the midpoint of the original triangle's edges. What you have left are three smaller triangles. Now do the same again with the smaller triangles. The cutting out is called an iteration. An iteration is a step which does a small part of the work and is done again and again to get the final outcome. The shape you end up with, the Sierpinski triangle, has a border which has a length of infinity: every time you repeat the above process you increase the length of the border by one half more than it just did on the last iteration (try it out on paper).
Now, if you have a regular triangle, you can easily describe each point which lies on the border
of the triangle with one number: For example, the distance you have to travel along the border starting
at one of the corners going clockwise. But how can you do this with the Sierpinski triangle? There are some
ways to go along the border of the Sierpinski triangle in one go, one you can see below which runs
on a Sierpinski triangle which has been drawn in 5 iterations:
But of course, a Sierpinski triangle drawn to five iterations is no real fractal because when you start to zoom in you'll pretty soon see no more selfsimilarity but just big areas of black and white. To get a real fractal, infinitely many iterations are needed.
So how can you describe a point which lies on the edge of the Sierpinski triangle? You may try to do it as in the regular triangle: use one number which says how far you have to move on the path -as you see it above- to get to the point. But there is one problem: the distance to a certain point depends on how many iterations were used when drawing the triangle. The distance can easily double if you do a couple more iterations. And for a Sierpinski triangle with infinite iterations the distance you have to go will be infinite for any given point.
So, you may try two numbers to show the location of
a point, for example, by using a coordinate system. So is the border of the Sierpinski triangle
two or one dimensional? Well, to describe a point on it you need at least two numbers, so in some
ways it's two dimensional, but still, a border is just a line without any thickness, so in that sense
it has a dimension of 1. From this it's clear that the border of the Sierpinski triangle doesn't have
a dimension of one or two, but a
non interger dimension somewhere between one and two.
You can find many fractal structures in nature.
A nice example is the cauliflower. A piece of it looks the same as the whole thing.
You can notice fractals in coastlines, mountains, clouds, trees and even in ferns!
Benoit B. Mandelbrot was born 1924 in Poland, but moved to France when he was twelve.
He researched on fractal structures and was the one to define their properties,
and to introduce the Mandelbrot Set, also known
as the Mandelbrot Bug, which is one of the most popular fractals.
You can make fractals out of any shape. A fractal is made by copying and altering the input image. A very simple example is a Pythagorean Tree. As the input image we take a square and attach a right triangle which shares its hypotenus with one side of the square. Then we add a square to each of the other sides of the triangle. Now we do the same for the smaller squares as we did for the first one. This way we can go on for ever and ever. We can repeat this to infinity! As a result we get the "Leafed" Pythagorean Tree.
Let's change it now a little bit: on each new square we will flip the right triangle. As a result we get the "Coniferous" Pythagorean Tree.
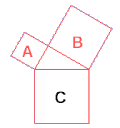
Did you know that for each iteration the sum of the area of the added squares is equal to the area
of the original square? You can easily prove
this with the Pythagorean theorem. The Pythagorean theorem proves that the square
A plus the square B equals the square C. So we know that the squares A and B have the same area
as square C on the right.
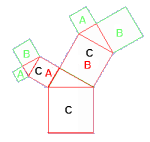
Now since a²+b²=c², we know that in the image on the right, both green squares A and B
added together have to have the same area as their corresponding square C. And since the red squares
A and B (the green C squares)
equal the big square C,
we can conclude that all of the green squares added together have the same area as the big square C.
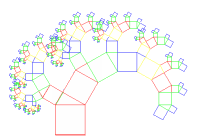From this we can conclude that this is true for every further step we make; every row of squares of the
same color added together equals the big square C.
If you haven't looked at the Pythagorean Tree Applets, look at them now!
"Coniferous" Pythagorean Tree
"Leafed" Pythagorean Tree
