Was nun kommt, macht besonders Spass: Die graphische Darstellung von Funktionen. Gewöhnlich benützt man dazu ein Koordinatensystem.

Descartes kam auf die geniale Idee, geometrische Figuren mit Hilfe von zwei einfachen Geraden zu analysieren. Wenn wir zwei Geraden mit einander kombinieren, bekommen wir ein Koordinatensystem. Nun können wir leicht jedem Punkt in der Ebene zwei Werte zuordnen, die sich ergeben, wenn wir vom Punkt aus das Lot auf die beiden Geraden fällen. Diese beiden Schnittpunkte definieren die Position des Punktes eindeutig.

Auch Fermat arbeitete mit dem Koordinatensystem. Er benützte es jedoch mehr in die andere Richtung; er zeichnete die Punkte ein, deren Werte eine bestimmte Gleichung erfüllen, und bekam so ein Bild für diese Gleichung. Das genau ist graphische Darstellung.

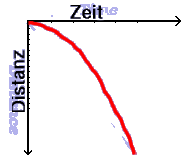
Rechts siehst du ein Beispiel. Dieser Graph zeigt dir, wo sich ein Körper im freien Fall gerade befindet, und zwar in Abhängigkeit von seiner Fallzeit. Dieser Zusammenhang kann mit der Funktion f(x)=x²×10 beschrieben werden, genau wie es Galileo entdeckt hat. Der Graph rechts ist so gezeichnet, dass du auf die Kurve treffen wirst, wenn du von einem Zeitpunkt auf der horizontalen Achse Zeit²×10 Einheiten senkrecht nach unten gehst.

Um eine trigonomterische Funktion darzustellen, können wir alles gleich machen. Wir benützen nun statt der Funktion f die Sinusfunktion.

Schau dir den Graph oben an. Wenn du mit der Maus darüber fährst, erscheint links ein roter Kreisbogen. Wir nehmen den Wert des Radius als 1 an. Dann entspricht die Länge des Bogens dem Winkel in Radiant.

Rechts vom Kreisbogen erscheint eine rote Linie. Sie hat immer dieselbe Länge wie der Kreisbogen. Darüber wird eine Kurve gezeichnet. Sie wächst gleichzeitig wie die rote Linie. Diese Kurve heisst Sinuskurve. Sie ist durch folgende Gleichung definiert: y=sin(x). Das heisst, dass für jeden Punkt auf der x-Achse ein Punkt gezeichnet wird, der um sin(x) überhalb der x-Achse liegt, wenn x die horizontale Distanz vom Achsenschnittpunkt ist.