Ein besonders interessanter Teil der Trigonomometrie ist die graphische Darstellung von Funktionen. Bevor wir das tun, wollen wir aber zuerst ein anderes Winkelmass anschauen.

Bis jetzt haben wir Winkel in Grad beschrieben. Diese Art Winkelberechnung ist sehr alt. Sie wurde schon vor 4500 Jahren von der Sumerern benützt und später von den Babyloniern übernommen, deren Zahlensystem auf 60 basierte, und nicht auf 10 wie das unsrige.

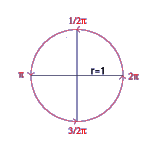
Um trigonometrische Funktionen graphisch darzustellen, ist es nützlicher, den vollen Winkel von 360° mit einem Kreis zu vergleichen, und ihm die Zahl 2πr zuzuordnen, die für den Umfang des Kreises steht.

 

Überlege dir diesen Zusammenhang: Wenn du eine Gerade hast, die eine volle Umdrehung macht, so entspricht der zurückgelegte Winkel einem vollen Kreis. Nehmen wir zum Beispiel einen Radius von 1. Der Kreisumfang ist 2πr, der Winkelbogen wird also 2π×1 sein, was 2π entspricht. Eine volle Umdrehung ist also 2π. Wenn du dieselbe Überlegung machst mit einem Radius von 2, 3 oder 4, wirst du für eine volle Umdrehung immer auf den gleichen Wert kommen.

Wie gross ist nun ein 180° Winkel, ausgedrückt in Radiant? π; das entspricht der Hälfte einer ganzen Umdrehung, welche 2π entspricht.