
| |
Mit der Zeit bekamen die am meisten benutzten Verhältnisse zwischen den Seiten und einem der spitzen Winkel in rechtwinkligen Dreiecken eigene Namen. Und da die Verhältnisse von der Grösse der Winkel abhängen, schrieb man Tabellen für viele verschiedene Winkel. Das Verhältnis, das Dido benützte um die Distanz vom Boot zum Festland zu berechnen, heisst Tangens.
Der Tangens eines spitzen Winkels in einem rechtwinkligen Dreiecks ist definiert als das Verhältnis zwischen Gegenkathete und Ankathete.
Der Tangens wird gewöhnlich mit tan abgekürzt.

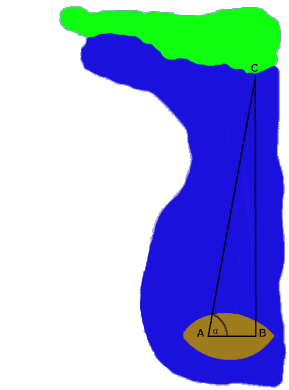
Im Bild oben ist der Winkel α bezeichnet, für den gilt: tanα=BC/AB.
(Mit BC und AB sind die Längen der Strecken gemeint, die B mit C bzw. A mit B verbindet.)
Dido hätte also kein Vergleichsdreieck abstecken müssen, sondern hätte einfach den spitzen Winkel auf dem Boot messen, den dazugehörigen Tangens nachschlagen, und ihn mit der abgestecken Strecke auf dem Boot multiplizieren können. Das hätte ihr die Distanz gegeben.
Dies hätte wunderbar geklappt, bis auf ein kleines Problem: Dido lebte
etwa 800 v.Chr. und die ersten heute bekannten Tabellen wurden etwa 140 n.Chr. geschrieben.
Du hast es gut, du brauchst nicht einmal eine Tabelle. Hol deinen Rechner. Dido hat für den spitzen Winkel 78.7° gemessen. Tippe 78.8 in den Rechner und drücke auf tan. Du wirst sehen, dass das etwa 5 gibt.
Im Dreieck links siehst du, dass tanα gleich dem Verhältnis BC:AB ist. Also gilt AB=tanα×BC. Da der tanα ungefähr 5 ist und AB 12m misst, ergibt das für BC 60m. Dido ist mit ihrer Methode zum gleichen Ergebnis gekommen.
|
|
