After some time, people started to name the ratios of sides in right triangles in relation to one of the acute angles. And since the ratios depend upon the size of the angle, they wrote tables filled with these ratios for different angles. The ratio Dido used to calculate the distance between her boat and the coast is called tangent.

 

In equations, tangent is usually just written as tan.

In the picture to the above, the tangent of angle A is equal to BC/AB.

(Note: BC and AB are the length of the lines connecting B with C and A with B)

Instead of drawing a second triangle and measuring its sides, Dido could have just measured the acute angle on the boat, looked up the tangent for that angle and multiplied it by the distance of the two points she had chosen on the boat and like this she would have gotten the distance her boat had from the shore.

This would have worked allright, except for one slight problem: the first trigonometric tables known today were written about 140 BC, and Dido lived way earlier, around 800 BC.

 

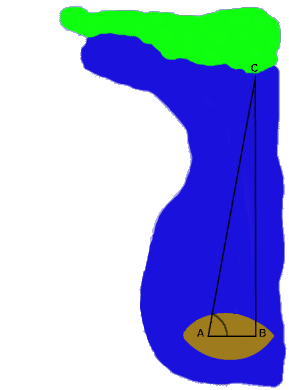
But you don't even need a table! Get your calculator! Dido found that the angle at A is about 78.7°. Enter the numbers of degrees into your calculater and then press on tan. You will see that the tangent of 78.7° equals about 5.

 

In the triangle to the left you can see that the tangent of angle A is equal to the ratio between the sides BC and AB. In our case AB=tanA×BC. Since tanA equals approximately 5 and Dido measured 32feet for AB, BC equals 160feet. This is the same result that Dido got using her method.