Graphing the trigonometric functions is one of the most interesting parts of Trigonometry. But first, we are going to look at another way to describe angles.

Until now, we have described the size of angles in degrees. Degrees were introduced by the Sumerians 4500 years ago. The Sumerians as well as the Babylonians later on used base 60, and not base 10 as we do. That's why we have a full circle defined as 360°.

To graph trigonometric functions, there is another more useful way to express angles. Instead of defining a whole revolution of one side of an angle as 360 units, we compare it with the circumference of a circle which is 2πr.

Radians measure the arc formed by an angle divided by the radius of the arc. A full rotation has a value of 2π.

Try it out. If you have a full rotation, the arc is a full circle, take for example a radius of 1 and the circumference will be 2π (1×2π). Divide that by the radius which in this case is 1 and you get 2π. So a full rotation is equal to 2π.
Try it with a radius of 2, 3, or 4. You will always get the same value for a full rotation; a circle with a radius twice as long will have an arc twice as long. For the size of an angle it doesn't matter at which distance the arc is. That's why we don't have to care about the radius. Note also that we don't need a unit to express radians; by dividing the circumference by the radius any type of unit will be canceled out, for example, if you divide &pi inches by 1 inch you get π.

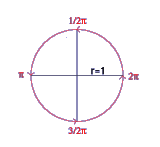
So how is a 180° angle written in radians? It's π, exactly half of a full rotation which is equal to 2π.