| |
Eine weitere Möglichkeit, die Realität besser zu beschreiben, gibt uns die Zuordnung von Elementen zu Fuzzy Mengen. Der Unterschied zwischen einer binären und einer Fuzzy Menge ist, dass bei der "normalen" Menge jedes Element entweder dazugehört oder nicht. Auch hier gilt wieder A oder Nicht-A. Zur Fuzzy Menge kann ein Element zu einem gewissen Grad dazugehören und gleichzeitig zu einem gewissen Grad nicht dazugehören.
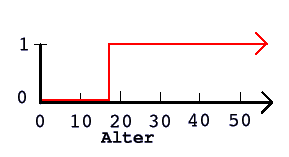Schauen wir uns ein Beispiel an: Wenn wir die Menge der Erwachsenen als binäre Menge illustrieren, kann
das etwa so aussehen wie im Bild rechts. Hier wird angenommen, dass man mit 18 erwachsen wird. Man könnte
sich natürlich darüber streiten, ob man dafür 21 Jahre wählen soll, und eventuell den Graph auf dieses
Alter abändern. Gleich bleiben würde dabei aber, dass jede Person entweder erwachsen ist oder nicht-erwachsen
ist, in der Darstellung 1 oder 0.
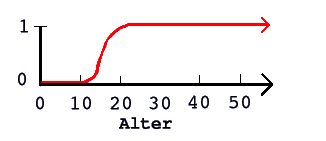Wenn wir den Graph der Fuzzy Menge der Erwachsenen skizzieren, könnte entwas heraus kommen wie
das Bild links. Hier haben wir einen fliessenden Übergang zwischen erwachsen und nicht-erwachsen. Auch
hier könnten wir wieder diskutieren, wie die Kurve gezeichnet werden sollte. Beginnt der Prozess des
Erwachsenwerdens vielleicht erst mit 13 und ist schon mit 19 zu Ende? Auf jeden Fall ist aber die Kurve
der Fuzzy Menge der Erwachsenen besser als die binäre; das Erwachsenwerden hängt nicht von einem Datum
ab. Wir gehen nicht an einem bestimmten Tag als Kind zu Bett und wachen als Erwachsene auf. Erwachsenwerden
ist ein kontinuierlicher Prozess, und kontinuierliche Prozesse können mit Fuzzy Mengen besser beschrieben werden.
