| |
Another way to describe reality more accurately is with the membership of fuzzy sets. The difference between a binary set and a fuzzy set is that in a "normal" set every element is either a member or a non-member of the set. Here again, we see that it either has to be A or not-A. In a fuzzy set, an element can be a member of a set to some degree and at the same time a non-member to some degree of the same set.
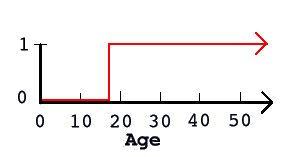Let's look at an example: if we want to illustrate the set of adults using a binary set, we get
a picture like the one to the right. In this picture it is assumed that a person becomes a grown-up
on his or her 18th birthday. Of course someone may argue that a person becomes an adult
with 21 and we'd have to change the graph. What would stay the same, however, is that every person
is either adult or non-adult, in the graph 1 or 0.
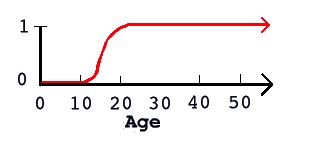When we graph the fuzzy set of adults, we get something like the picture on the left.
Here, there is a gradual process between being adult and non-adult. Again we can argue how exactly the
curve should be drawn. Someone may say a 13 year old is completely non-adult or that a 19 year
old has to count as an adult. But we can be sure that the fuzzy curve of the set of adults is closer to the truth
then the binary curve; we all agree that we can't give a specific date when people turn into adults.
It's not like we go to bed one day as a child and wake up the next as an adult. Growing up is a
gradual process and gradual processes can better be described with fuzzy sets.
