| |
Auch die arithmetische Formulierung des Beweises ist aus den obigen Bildern leicht ableitbar:
Wir bezeichnen die Katheten mit a beziehungsweise b, die Hypotenuse mit c.
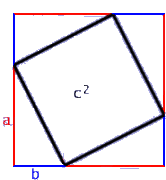
Die Fläche des zweitletzten Bildes kann auf zwei Arten berechnet werden:
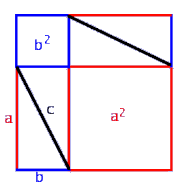
I. a2+b2+4ab/2 = (a+b)2
Das letze Bild zeigt:
II. c2+4ab/2 = (a+b)2
Die rechten Seiten von Gleichung I und II sind gleich.
Daraus folgt, dass auch die linken Seiten gleich sein müssen.
a2+b2+4ab/2=c2+4ab/2
Wir können nun auf beiden Seiten 4ab/2 wegzählen und bekommen die berühmte Formel:
a2+b2=c2
