


| |
Sicher ist dir aufgefallen, dass Smart Joe eine eher ungewöhnliche Art zu rechnen hat. Es gibt aber Situationen im Leben, wo wir alle seine Methode benützen, und auch in einigen Gebieten der Mathematik wird sie manchmal bevorzugt.
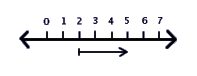
Unsere übliche Art zu rechnen kann auf einer Zahlengerade graphisch dargestellt werden. Das Bild auf der linken Seite zeigt zum Beispiel die Aufgabe 2+3=5. Die beiden Pfeile deuten an, dass die Linie und die Zahlen darauf theoretisch immer weiter gehen.
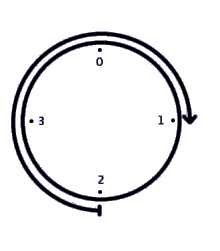
Um graphisch zu zeigen, wie Smart Joe Rechnungen löst, brauchen wir nicht eine Linie, sondern einen Kreis. Links stellen wir auf einer Vierer-Uhr (aus Smart Joes umfangreicher Sammlung) 2+3=1 dar. Diesmal fehlen die Pfeile, die im obigen Bild die Unendlichkeit darstellen, denn im Uhrensystem haben wir eine festgelegte, endliche Menge von Zahlen.
Wie du siehst, gibt es zwischen unserer und Smart Joes Art zu rechnen einen
entscheidenden Unterschied: Er benützt ein endliches Zahlensystem, während
wir ein unendliches benützen.
Im Alltag verwenden jedoch auch wir oft sein System, zum Beispiel bei der Uhr.
Bei der Uhr ist es uns klar, dass nach der 12 wieder die 1 kommt und es interessiert sich niemand dafür, wieviele Male der Zeiger schon herum gegangen ist. Sonst würden wir eine Antwort wie "Es ist 17'537'520 Stunden nach Christi Geburt" bekommen wenn wir nach der Zeit fragen.
Es gibt auch andere Fälle, in denen wir ein Uhrensystem benützen, zum Beispiel beim Kompass. Nehmen wir an, du schaust auf den Kompass während du nach Norden gehst. Du folgst immer der Nadel. Dann machst du eine ganze Drehung. Die Nadel zeigt wieder nach Norden. Dem Kompass siehst du nicht an, dass du soeben eine ganze Drehung gemacht hast. Zum Glück! Stell dir vor, du würdest 1085 Grad ablesen! (Welche Richtung wäre das übrigens?)
