


| |
Smart Joe doesn't solve his calculations as most of us do, and he doesn't always get the same answers. But sometimes in life and in mathematics his approach is the preferred one.
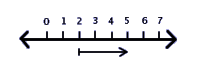
When we solve a problem in our usual way, we can show it graphically using a number line. For example if we have the problem 2+3=5 we can show it with a picture like the one on the right. The arrows on both ends of the line show that it would theoretically go on for ever.
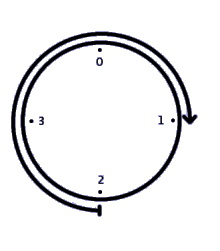
If we want to show a problem the way Smart Joe solves it, we have to show it on a circle instead of on a line. In his extensive collection of watches he has one that goes up to 3. On the left you can see how to visualize the problem 2+3=1 on that watch. As you see, this time there are no arrows to show infinity. That's because on a clock there's a defined amount of numbers.
As you can see here, there's a major difference between our usual way of
calculating and Smart Joe's. We use an infinite system while he uses finite systems.
But even we sometimes use finite systems. The most commonly used one is of course the
normal clock.
When we use a clock it seems natural that a 1 comes after the 12. And it also seems natural that we don't try to keep track of how many times the clock went around before. Otherwise we might get an answer such as "it's 17'537'520 hours since the birth of Christ" when we ask someone for the time.
Of course there are many other cases where the clock systems are used. For example, when we use a compass. Say you are looking at the compass and walking north. You always follow the needle. Now you walk a complete circle. You take another look at the compass. It still points the same way. By looking at the compass there is no way to tell that you just did a complete turn. Luckily! How would you like to read 1085 degrees on your compass? (What direction would you be facing?)
