As you have seen on the previous page, triangles with equal angles have equal ratios between their sides. This has been known for a long time. The Egyptians already used these relations to calculate for example the sizes and distances of heavenly bodies.

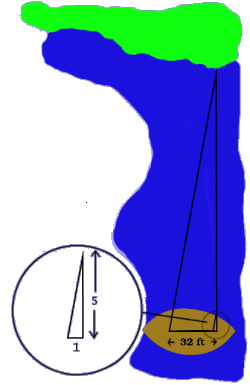Dido is on her way to Africa and would like to know the distance from her boat to the mainland. First she chooses two points on the boat and one on the mainland. Then she measures the angles of the triangle formed by these three points. After that she constructs a triangle with exactly the same angles on the boat and measures its sides.

In this example the longer one of the legs has a length of 25 feet. The shorter one at the bottom has a length of 5 feet. The ratio between these sides is 5:1 which, since a ratio is just a fraction, equals 5. Once you know this, it is clear that the longer side is five times longer than the shorter.

Dido's next step is to measure the shortest side of the large triangle. It has a length of 32 feet. To find the distance from the mainland to the island, Dido just has to find a number which is five times bigger than 32. By multiplying 32 with 5 she gets 160.

Now Dido knows that the distance from the boat to the mainland is 160 feet.