| |
In modular arithmetic you can also write equations such as 4 mod 8 = 12 mod 8. Take another look at this equation. Is it correct? (You can think of 4 mod 8 like a watch with eight instead of twelve numbers (0 at the top), with a hand pointing toward the 4. For 12 mod 8 you have the same kind of watch. To show 12 on this watch the hand has to do twelve steps starting at 0. To accomplish this, the hand has to do a whole turn (eight steps) and stop four steps later pointing to the 4. Since the hands point at the same number both times, you can conclude that the above equation is correct.)
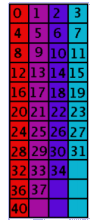In the first row of the table on the left you can see all the elements of mod 4
(or the four hour watch). Beneath each of the numbers are all the whole numbers
which equal the first number if you take them mod 4. For example, you can see
that there's a 0 at the top of the red column. Beneath you'll find 4,8,12,etc.
since 4 mod 4 equals 0, 8 mod 4 equals 0 etc. In the purple column there's a
1 at the top and beneath is every number where x mod 4 equals 1 (5,9,13,...).
In the dark blue column x mod 4 equals 2 and in the light blue column x mod 4
equals 3. You can easily see that theoretically these columns go on for
ever.
Now take a look at the table on the right. This table illustrates mod 7 (in the
top row are all the elements of mod 7).
You can see that in the table on the right, the red column shows
all the numbers where x mod 7=0. In the table on the left the red column illustrates
x mod 4=0. Even though you could express both of these equations with the
equation x mod y=0 the numbers you find in the red columns differ quite a lot.
This special quality you find only in modular arithmetic.
Take a look at the interactive mod 9 converter below. Just enter a number and click on "GO". It will start to count downwards, moving one tick every time it subtracts one. As soon as it shows 0, the needle will point to the result. If you enter 10 for example, the hand will go once around and one tick further, so it will stop at 1. If you enter 12 the hand will also go around once and it will stop at the 3.
Try out some different numbers. For example, 1,10,2,11,20,3,12,21. Do you see a pattern?
There is a pattern for mod 9! For x mod 9 you can just add all the digits of x together. Do the same with any results bigger than 10 until you get a number that is smaller than 10. If you get 9, convert it to 0. If you have 2153 mod 9 for example, you add the digits together and you get 11. Now you do the same for 11 and you get 2. That means 2153 mod 9 = 2.
