



| |

Take a look at this right triangle: we need to prove that the area of the purple square has the same size as the areas of the blue and red squares added together.
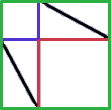
In this image you can see that the large green square has sides which are the same length as the two legs (red and blue) of the triangle combined together. In addition to the two squares there are four triangles which have the same size as the one you saw above.
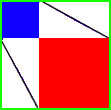
Now check out this new image. The blue square, the red square, and four right triangles are in it.

In this last image you can see four right triangles.Their hypotenuses form the purple square.
Since the green squares in the last two pictures have the same size, and they each contain four identical triangles, the red and the blue square combined must have the same area as the purple square. That's just what we wanted to prove.
